El problema de Container With Most Water (Contenedor con más agua) es un problema de programación que puedes encontrar en LeetCode que trata de encontrar el contenedor con más agua que puede encontrarse en una lista de números enteros. Aquí analizaremos el problema y veremos qué preguntas nos debemos hacer para poder resolverlo, además de una solución en Rust 🦀.

Análisis del problema

Como en todos los problemas de programación, lo primero que debemos hacer es analizar el problema, entender qué es lo que nos están pidiendo y qué datos nos están dando.

Qué recibiremos en el input?

• Recibiremos una lista de números enteros.
• La lista tendrá al menos 2 elementos y como máximo 10⁵ elementos (100,000 elementos).
• Cada número entero de la lista representa la altura de la columna de esa posición.
• El valor de cada elemento podrá estar entre 0 y 10⁴ (10,000).

Qué significa “el contenedor con más agua”?

Qué es un contenedor?

• Un contenedor es una figura geométrica que tiene una base y una altura, para efectos prácticos del problema podemos decir que nuestro contenedor tendrá la figura de un rectángulo.

En este rectángulo, la base será la distancia entre las dos columnas que estemos comparando y la altura será el valor de la columna más pequeña. Usamos la columna más pequeña porque si usamos la más grande el agua se derramará.

Sabiendo lo anterior, cómo sabemos cuál es el contenedor con más agua?

• El contenedor con más agua será el que tenga el área más grande.
• El área de un rectángulo se calcula multiplicando la base por la altura A = base * altura.

Planteamiento de la solución

Ahora que sabemos qué es lo que nos están pidiendo y qué datos nos están dando, podemos plantear una solución.

Qué estrategia podemos usar para encontrar el contenedor con más agua?

Una estrategia de fuerza bruta podría ser comparar cada elemento con todos los demás que están a su derecha, midiendo la distancia entre ellos y multiplicando por la altura de la columna más pequeña.

fn max_area(height: Vec<i32>) -> i32 {
    let mut max_area = 0;
    for i in 0..height.len() {
        for j in i + 1..height.len() {
            let area = (j - i) * height[i].min(height[j]);
            max_area = max_area.max(area);
        }
    }
    max_area
}

Esta solución, aunque funciona, no es eficiente porque está anidando dos bucles for que recorren toda la lista. Lo que nos deja una complejidad temporal de O(n^2).

Qué estrategia podemos usar para mejorar la eficiencia de la solución?

Podemos usar la estrategia de Dos punteros (Two Pointers) para mejorar la eficiencia de la solución. Con esta estrategia, vamos a tener un puntero que empezará en el inicio de la lista y otro al final. Comparamos las alturas de las columnas, calculamos el área y movemos el puntero que tenga la menor altura hacia el siguiente elemento.

Por qué esta estrategia es mejor?

• Nos ahorramos de recorrer toda la lista varias veces, vamos a recorrerla solo una vez.
• No estamos haciendo comparaciones innecesarias, vamos a comparar las alturas de las columnas y a mover el puntero que tenga la menor altura hacia el siguiente elemento.

La solución en Rust quedaría así:

pub fn max_area(height: Vec<i32>) -> i32 {
    // Inicializamos el área máxima en 0
    let mut max_area = 0;

    // Inicializamos los punteros en el inicio y en el final de la lista
    let mut left: usize = 0;
    let mut right = height.len() - 1;

    // Recorremos la lista mientras el puntero izquierdo sea menor que el puntero derecho
    while left < right {
        // Calculamos la diferencia entre los punteros, esto nos dará la base del rectángulo
        let diff = right - left;

        // Obtenemos los números de las columnas
        let left_number = height.get(left).unwrap();
        let right_number = height.get(right).unwrap();

        // Obtenemos la altura máxima posible para el rectángulo
        // Si ambas alturas son iguales la que se estaría usando sería la izquierda
        let max_possible_height = left_number.min(right_number);

        // Calculamos el área del rectángulo
        let result = max_possible_height * diff as i32;

        // Actualizamos el área máxima si el área del rectángulo es mayor que la máxima actual
        max_area = max_area.max(result);

        // Movemos el puntero que tenga la menor altura hacia el siguiente elemento
        // Si la columna izquierda es menor que la derecha, movemos el puntero izquierdo hacia la derecha
        // Si la columna derecha es menor que la izquierda, movemos el puntero derecho hacia la izquierda
        // Si son iguales, movemos el puntero izquierdo hacia la derecha
        match left_number > right_number {
            true => right -= 1,
            false => left += 1,
        }
    }

    // Retornamos el área máxima
    max_area
}

En la siguiente animación podrás ver cómo funciona la solución anterior.

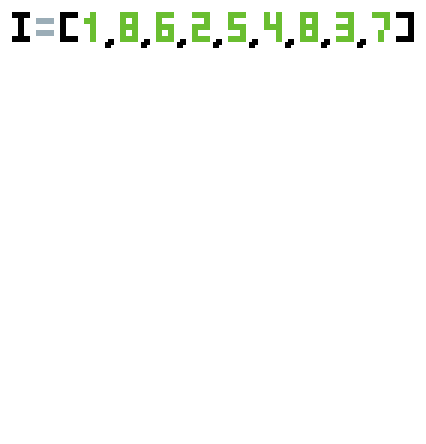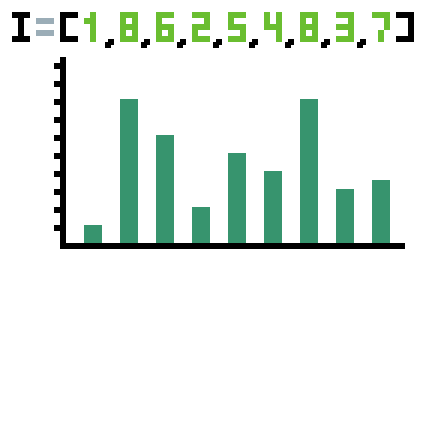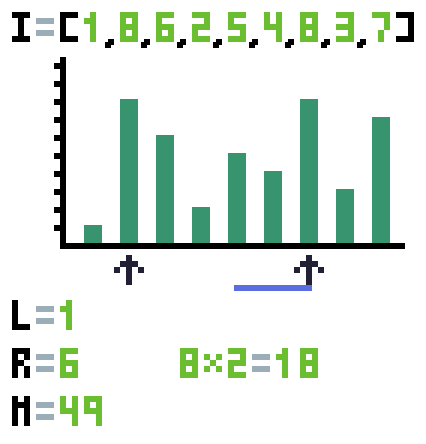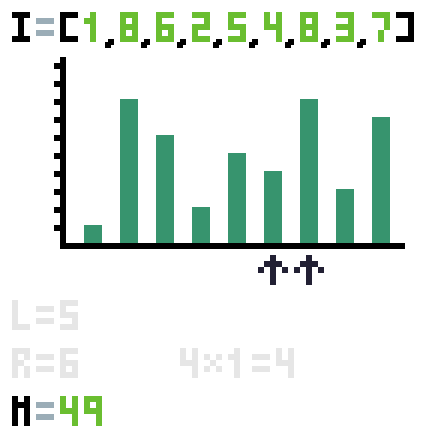
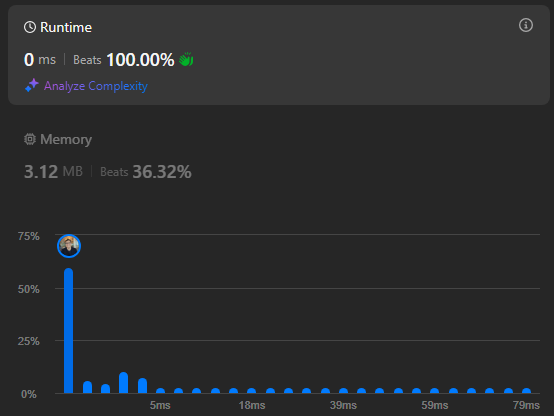
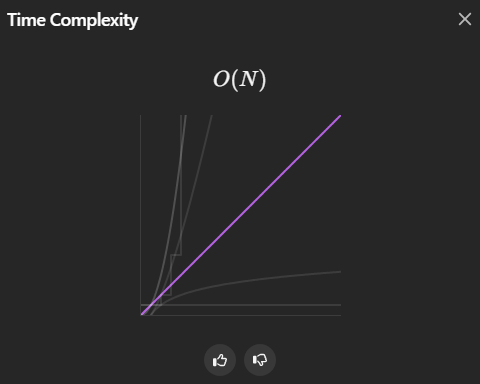
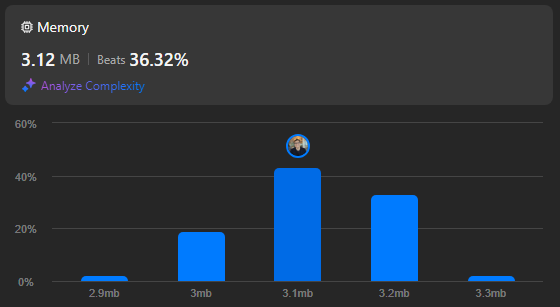
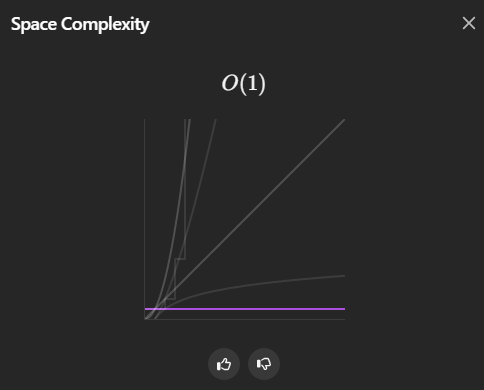
Resultados de la solución

La solución anterior tiene una complejidad temporal de O(n) y una complejidad espacial de O(1).